Chessmetrics Ratings: 81st Birthday

#	Player	Rating	+/-
1	Najdorf, Miguel	2525	65
2	Reshevsky, Samuel H	2495	66
3	Mieses, Jacques	2316	75
4	Zhukhovitsky, Samuil M	2277	73
5	Denker, Arnold S	2229	67
6	Wagman, Stuart	2177	59

About these ratings

All players on their 81st birthday

#
Player Rating +/- Best? 75%? Rating Date

1 Najdorf, Miguel 2525 65 62.0% #2 03/31/1991: #229

2 Reshevsky, Samuel H 2495 66 37.3% #2 10/31/1992: #367

3 Mieses, Jacques 2316 75 0.5% #4 12/31/1945: #64

4 Zhukhovitsky, Samuil M 2277 73 0.2% #5 11/30/1997: #2640

5 Denker, Arnold S 2229 67 #5 01/31/1995: #2937

6 Wagman, Stuart 2177 59 #6 05/08/2000: #3416

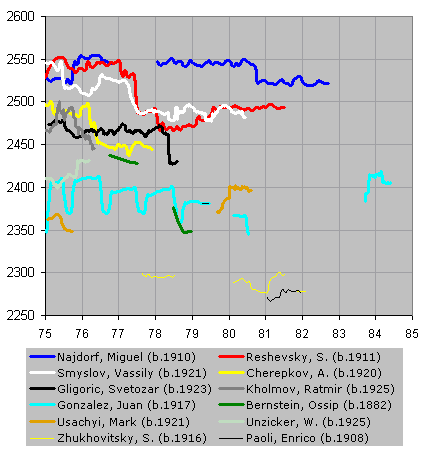
For each player on this list, the rating they possessed on their 81st birthday is listed. That rating was the last one calculated while they were 80 years of age, so it was their "current" rating on the day they turned 81. Players who played an insufficient number of games in recent years will not appear on the list, even though you may see them on lists for younger and/or older birthdays. Any players who had been completely inactive for three years are removed from the list.

Definition of columns in the above list:

# refers to the player's all-time rank on this list, compared to all other players when they turned 81.

Player is the full name of the player. Click on the player's name to see a career progression of their ratings.

Rating is the calculated rating for each player on their 81st birthday.

+/- is the standard deviation of the player's rating estimate. It is based on a geometric average of the number of rated games played in past years. Players who play very frequently will have a smaller +/- value, indicating a greater confidence in the accuracy of their rating. Players whose +/- value exceeds 76 are classified as "inactive" and removed from the ranking list due to their infrequent play against rated opponents. Mathematically, a player's rating is an estimate of their exact strength on their 81st birthday. The +/- value represents the standard deviation of that estimate; the player's true strength on their 81st birthday should be within one standard deviation of their calculated rating approximately 68% of the time, and within two standard deviations of their calculated rating approximately 95% of the time.

Best? is the estimated likelihood that the player was stronger on their 81st birthday than anyone else turning 81. Since ratings are known to be inaccurate, it is possible that a lower-rated player was actually much stronger than their rating would indicate, and it is also possible that other players were weaker than their ratings would indicate. This number indicates the likelihood that the player was indeed the strongest player ever among players turning 81. On a particular list, it will add up to 100% across the complete list of all players. This value is only calculated for the top 100 players on any rating list.

75%? gives a 75%-confidence world ranking for the player. Because ratings are known to be inaccurate, even if a particular player had the third-highest rating ever, among players turning 81, we cannot say with 100% certainty that they were truly one of the three strongest 81-year-old players. This number indicates the all-time rank that we are 75% sure the player is "no worse than". Thus if a player has a value of #12 in this column, we are 75% sure that the player is one of the twelve strongest players ever to turn 81. This value is only calculated for the top 100 players on any rating list.

Date is the exact date that the rating applied to. Click on that date to see the sorted list of all players' ratings on that date.